Százalékszámítás

Előzetesen annyit mondanék el, hogy a százalékszámítás, ahogy az arányossági feladatok is, többféleképpen magyarázhatók. A százalékszámítást az egyenes arányosságnál megtanultakra építem. Azt pedig – legtöbb kollégámtól eltérően – az egységre való visszakövetkeztetés kihagyásával tanítom, azt állapítjuk meg, a mennyiség hányszorosára változik. Ez első látásra bonyolultabbnak tűnik, mintha egységre következtetnénk, viszont tapasztalataim szerint az algoritmust hamar megtanulják és jól használható az arányossági feladatoknál (fordított arányosságnál kifejezetten szemléletes, hiszen az egyik mennyiség változása a másik mennyiség reciprokszoros változását vonja maga után), a százalékszámításos feladatok esetén nem kell képleteket megjegyezni, nem keverik össze, mikor kell szorozni az 1%-ot kitevő mennyiséggel és mikor kell osztani vele; de a kémiai számításos feladatoknál is jól használható. Természetesen a jobb képességű tanulókkal más megoldási lehetőségeket is alkalmazunk.

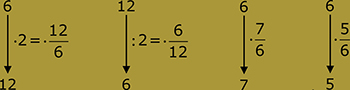
1. feladatsor

A százalék fogalma

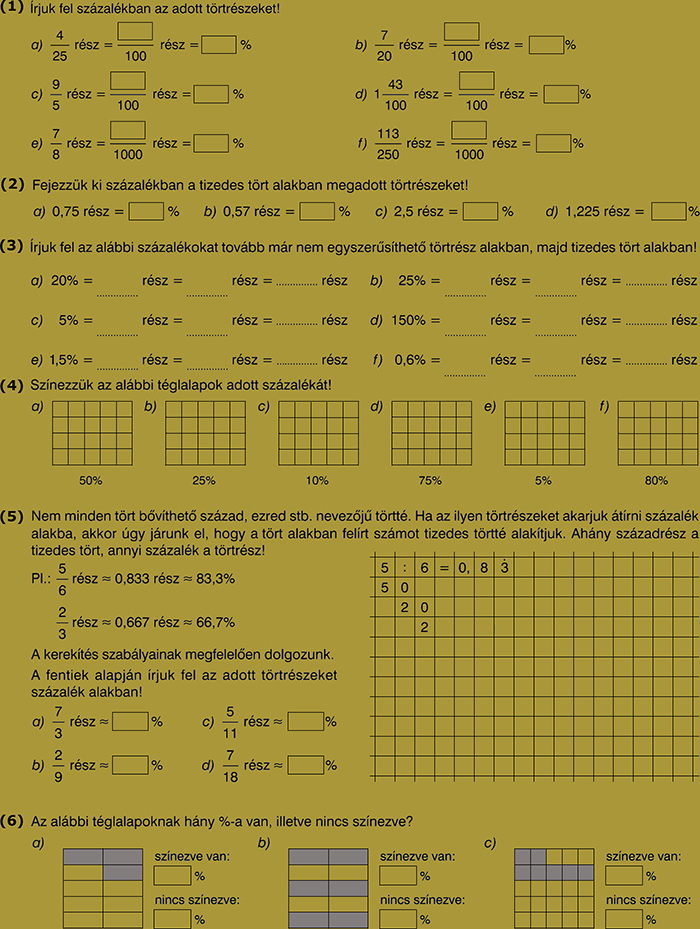
2. feladasor

Érték, százalékláb, alap kiszámítása arányos következtetéssel

3. feladatsor

4-5. feladatsor

Mivel a téma átfedi az „Arány, arányosság” témakört is, így a következő két feladasor ott is megtalálható. Ha megtekintenéd őket, akkor kattints ide: 4. feladasor, 5. feladatsor.

6. feladatsor

A „Műveletek, arány, százalék” témazáró dolgozata szintén tartalmaz százalékszámításos feladatokat. Itt találod.