
Kerület, terület
1.
Elméleti összefoglaló
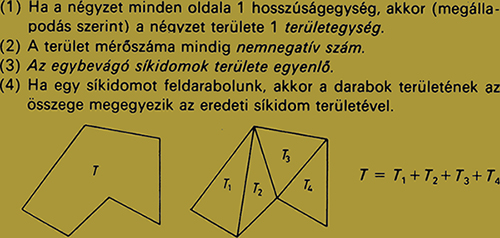
Terület fogalma: síkidomhoz rendelt mérőszám, megmutatja, hogy a síkidom mekkora helyet foglal el a síkból, hány db. területegységgel fedhető le hézagmentesen.
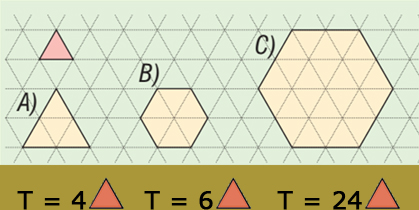
A síkidomok területét azonban nem háromszögekkel vagy egyéb tetszőleges alakzatokkal mérjük meg, hanem olyan négyzetekkel, amelyekek oldalai valamilyen SI hosszmértékegységgel adottak:
A területmérés alaptételei (axiómái):
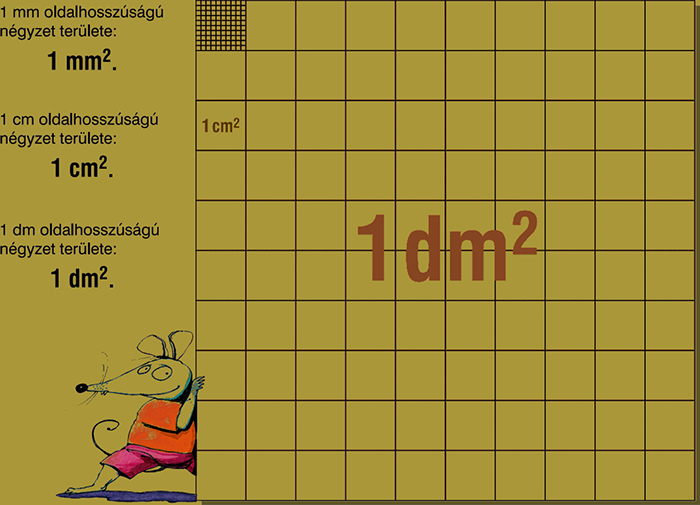
A területmérés mértékegységei:

Mit kell ismerned a helyes mértékváltáshoz?
- A mértékegységek közötti váltószámokat.
- A mérőszám és a mértékegység fordítottan arányos viszonyát.
- 10 hatványaival történő szorzás és osztás módját

2. feladatsor

3.
Speciális négyszögek területe

Korábbi tanulmányaitokból ismert, hogy a téglalap területe az egy csúcsba futó élek szorzataként számítható ki: T = ab.
A többi speciális négyszög területe ebből vezethető le:
| háromszög | paralelogramma |
 |
 |
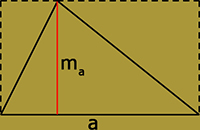
| Minden háromszög átdarabolható egy téglalappá, amelynek területe kétszer akkora, mint a háromszög. | Minden paralelogramma átdarabolható egy vele egyenlő területű téglalappá, amelynek egyik oldala megegyezik a paralelogramma oldalával, a másik oldala pedig a paralelogramma magasságával. |
| deltoid | trapéz |
 |
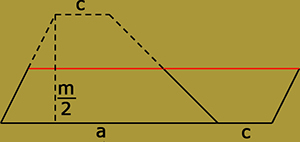 |
| Minden deltoid átdarabolható egy vele egyenlő területű téglalappá, amelynek egyik oldala megegyezik a deltoid egyik átlójával, a másik oldala pedig a deltoid másik átlójának felével. | A trapéz területét nem téglalapra, hanem a paralelogrammára vezetjük vissza. Mint látható, ha egy trapézt a középvonala (a szárak felezőpontja által meghatározott szakasz) mentén elvágunk, akkor az egy vele egyenlő területű paralelogrammává alakítható. A paralelogramma egyik oldala megegyezik a trapéz alapjainak összegével, a magassága pedig a trapéz magasságának felével. |
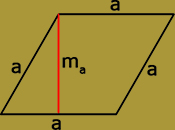
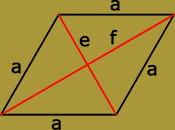
| rombusz | |
| mint speciális paralelogramma | mint speciális deltoid |
 |
 |
Mind e területképletek, mind pedig a képletek levezetése egy animált power point formájában letölthető.
Kör kerülete és területe
A kör – mint a legszabályosabb síkidom – már az ókori matematikusok érdeklődésének középpontjában állt.
A kör kerületét egyre finomodó sokszögek sorozatával közelítették:
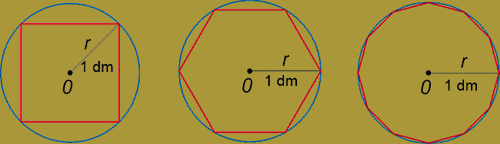
Összefüggést fedeztek fel a körök kerülete és az átmérője között. Bármekkora kört vizsgáltak, a kerületük és az átmérőjük hányadosa ugyanazt azt értéket vette fel. Ezt a nevezetes állandót a görög ![]() betűvel (pí) jelölték. Közelítő értéke 3,14.
betűvel (pí) jelölték. Közelítő értéke 3,14.
A kör kerülete: ![]() (r: sugár, d: átmérő)
(r: sugár, d: átmérő)
Ha egy kört egyenlő cikkekre osztunk és a rajzon látható módon helyezzük őket egymás mellé, akkor egy paralelogrammához hasonló alakzatot kapunk. Minél több cikkre bontjuk, a közelítés annál pontosabb. A rajzról látható, hogy a kapott paralelogramma egyik oldala a kör félkerületével egyezik meg, a magassága pedig a kör sugara:
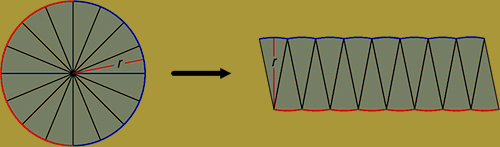
Tehát a kört átdaraboltuk egy vele egyenlő területű paralelogrammává:
![]()
4. feladatsor

5. feladatsor

6. feladatsor

7. feladatsor
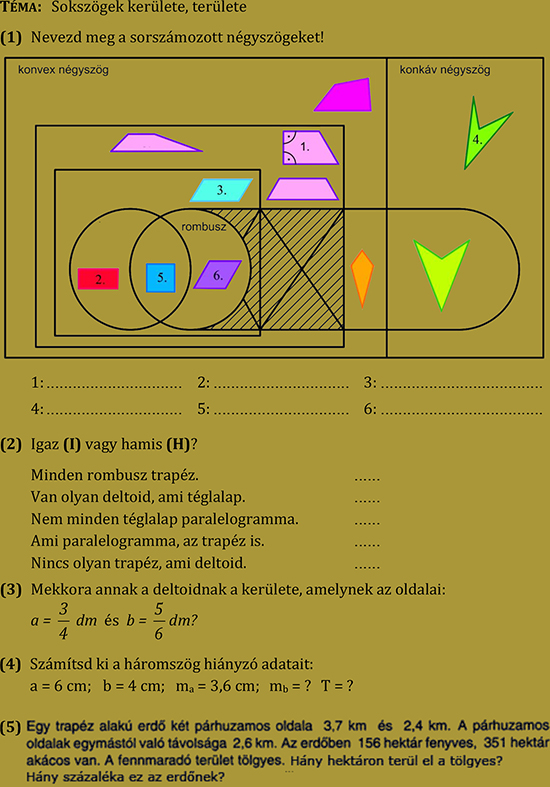
8. feladatsor

9. feladatsor

10. feladatsor
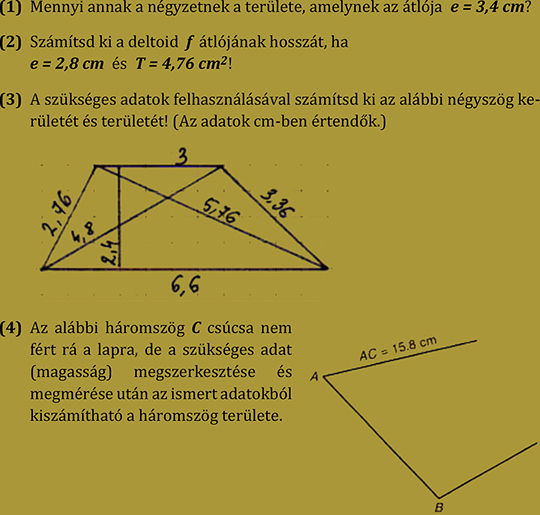
11. feladatsor

12. feladatsor

13. feladatsor

14. feladatsor
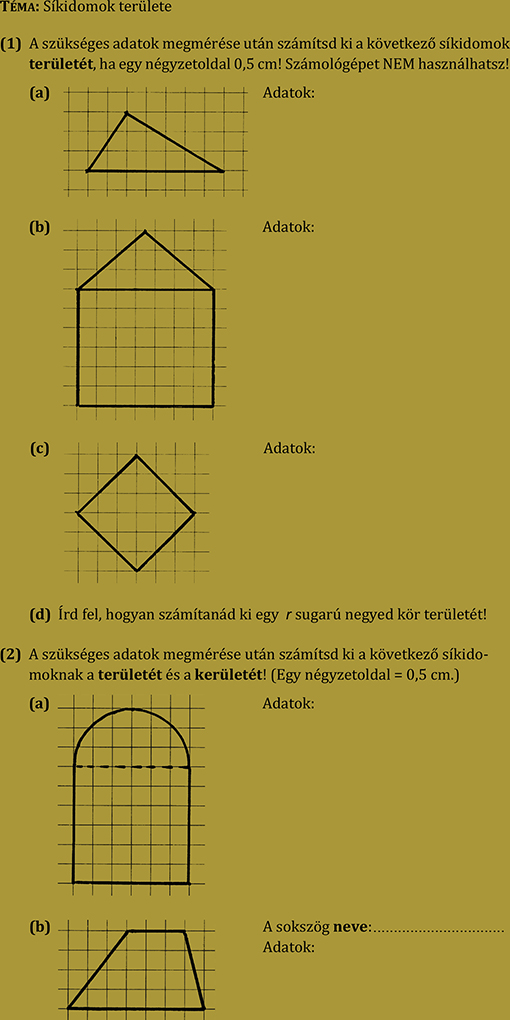
15. feladatsor

