Függvények
Pályafutásom elején megszenvedtem a „Függvények” téma tanításával. Valahogy nem állt össze bennem, és ez érezhető volt a gyerekek tudásán is. Átgondoltam, hogyan kellene egymásra építeni az ismereteket, ami reményeim szerint érthetőbbé teszi a témakört.
Így a feladatsorok mellett ebben a témában is közzéteszem a magyarázataimat, egyéb anyagaimat. Talán segítek vele másoknak is.
Az itt szereplő anyag nem teljes, pl. ezen a helyen nem szólok a nulladfokú függvényekről, a lineáris függvény fogalmáról. De nem is az volt a célom, hogy egy új könyvet írjak, csupán néhány fejezethez állítottam össze magyarázatot.
Lehet, hogy egyes feladatok ismétlődnek. Ennek oka, hogy ezek többnyire komplett feladatsorok, amelyeket gyakorlásra vagy számonkérésre használtam fel az oktató munkám során. Elkészítésükkor természetesen visszanyúltam a korábbiakhoz, itt-ott megváltoztatva, kiegészítve azokat, hiszen igyekeztem alkalmazkodni a tanulócsoportokhoz. Többnyire figyeltem, és a korábban már szereplő feladatokat kihagytam, de ismétlődések minden igyekezetem ellenére előfordulhatnak. De mint tudjuk, az ismétlés a tudás anyja … ![]()
1.

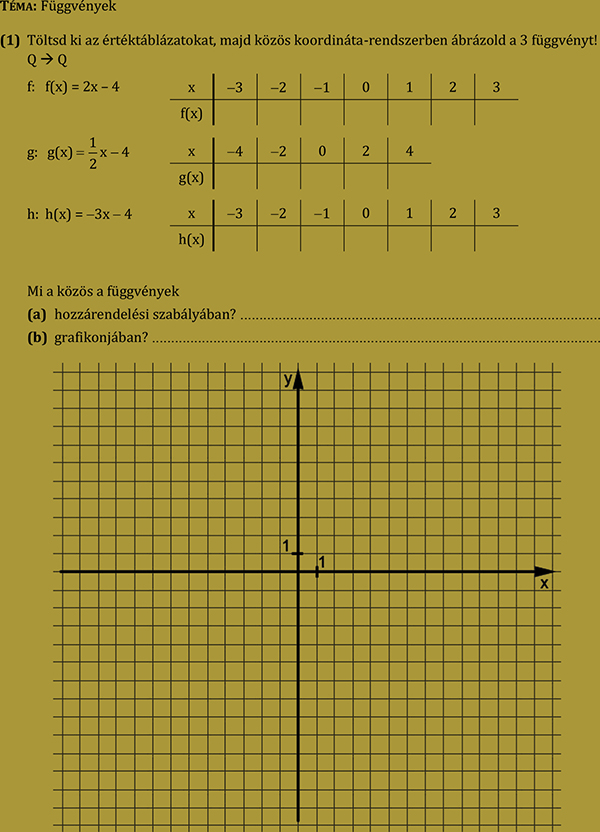
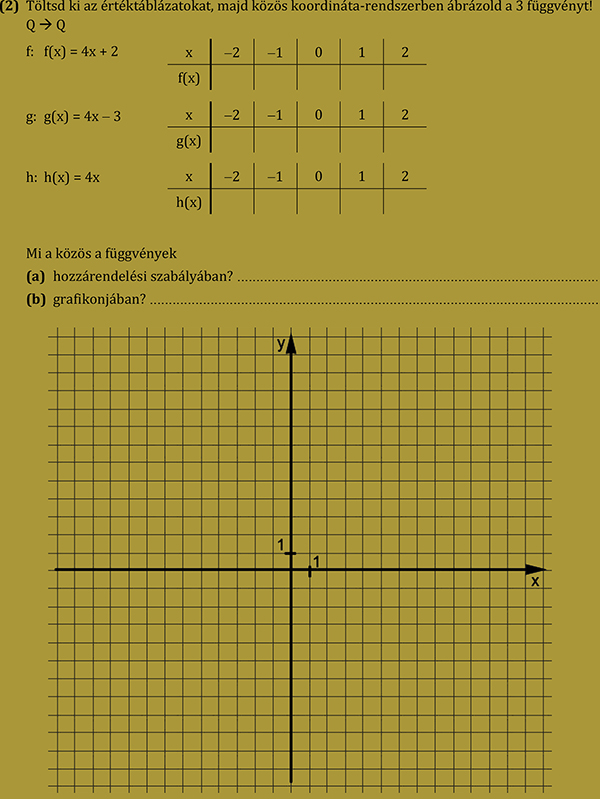
2. feladatsor


3. feladatsor
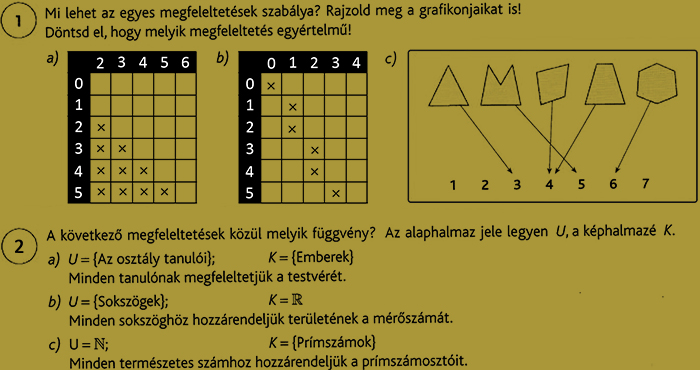

4. feladatsor




5.


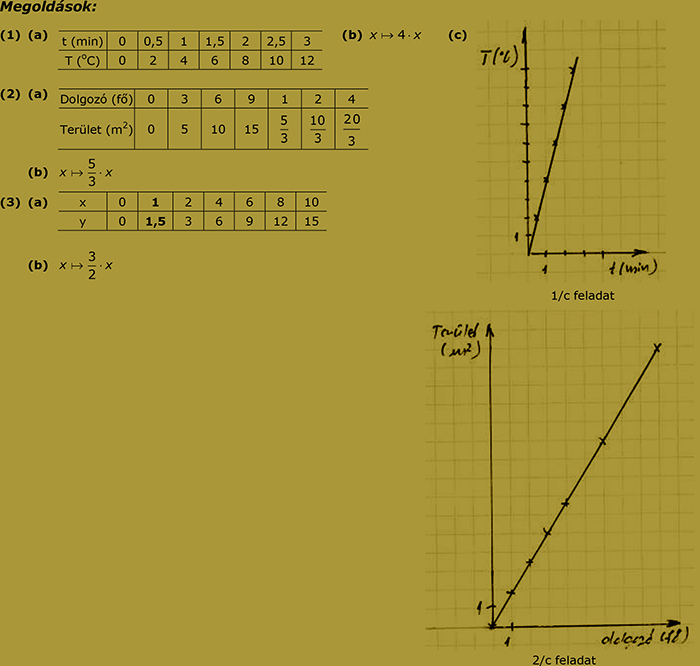
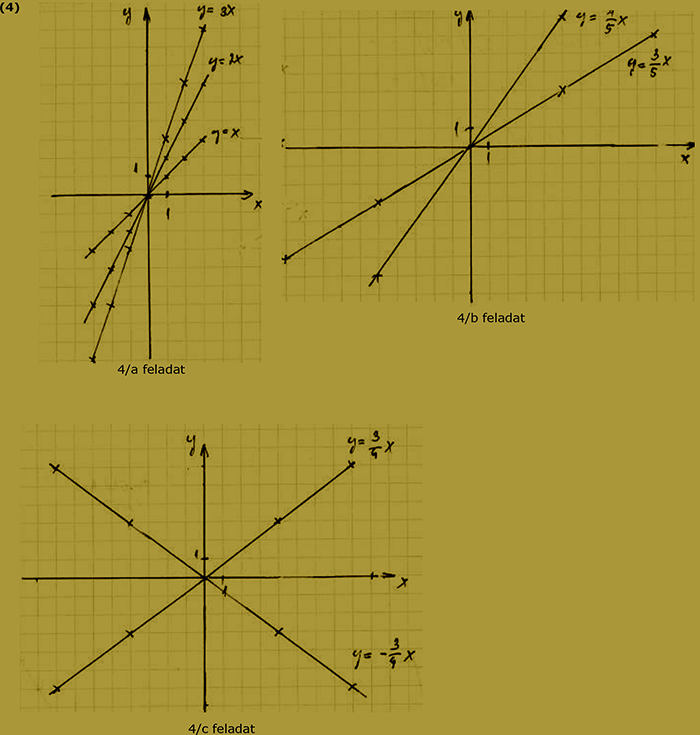
6.
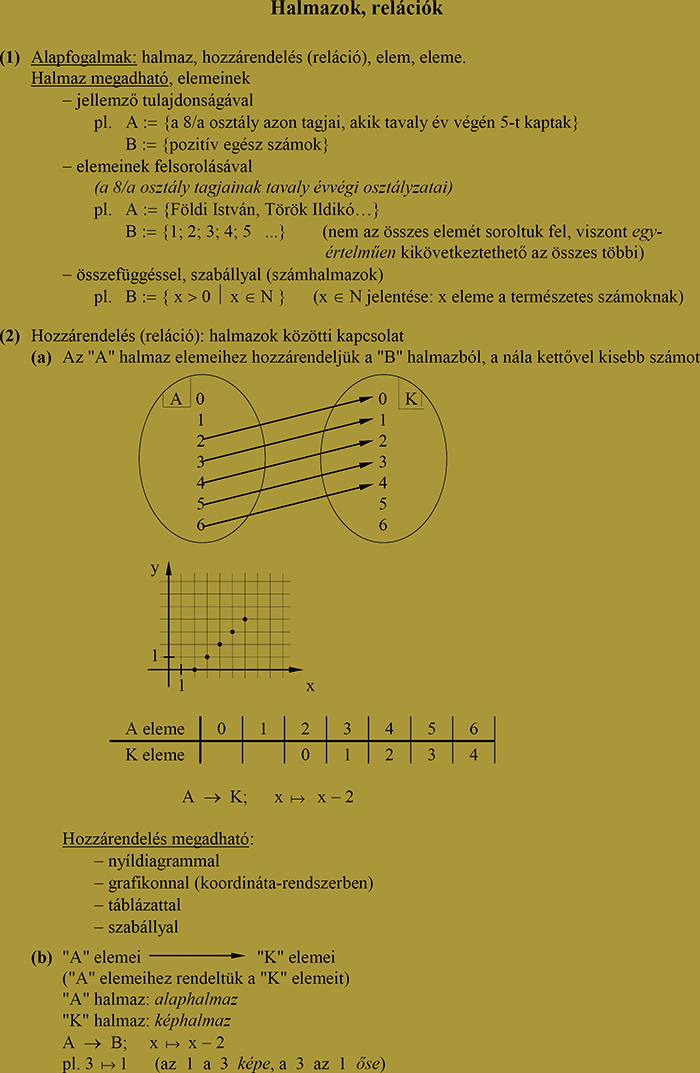
Egyenes arányosság ábrázolása táblázat nélkül
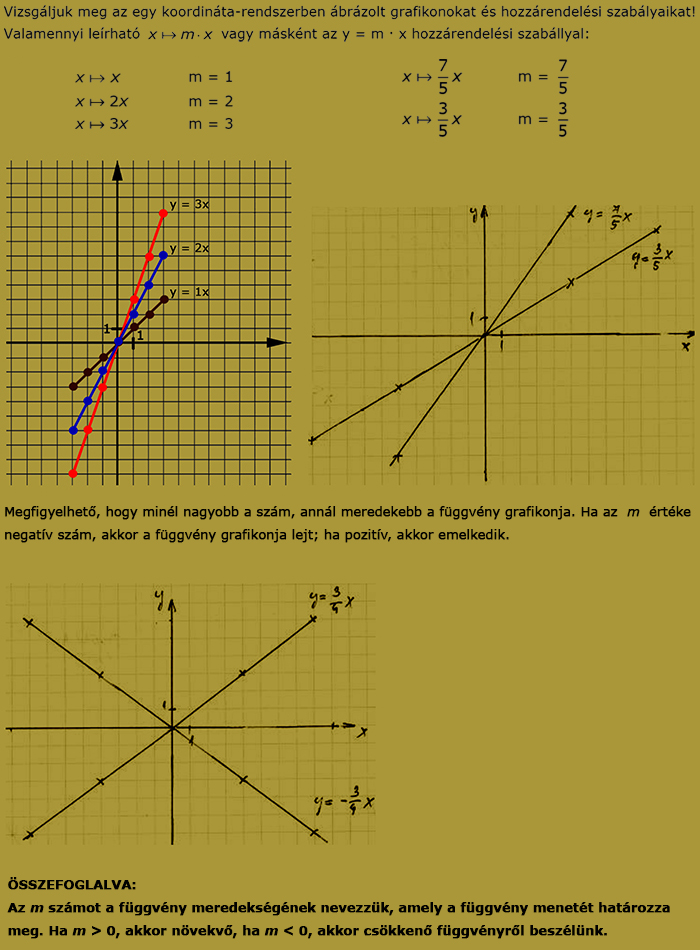
Az előzőekben megállapítottuk, hogy a már régről ismert egyenes arányosság is egy függvénykapcsolat. Mint ilyen, leírható egy hozzárendelési szabállyal. Ennek általános alakja: y = mx.
Mivel a függvények grafikonjai szintén alkalmasak a függő és a független változó kapcsolatának leírására, így a szabály és a grafikon kapcsolatát felismerve a táblázatba foglalt értékek kiszámítása nélkül is ábrázolhatjuk az egyenes arányosságokat.
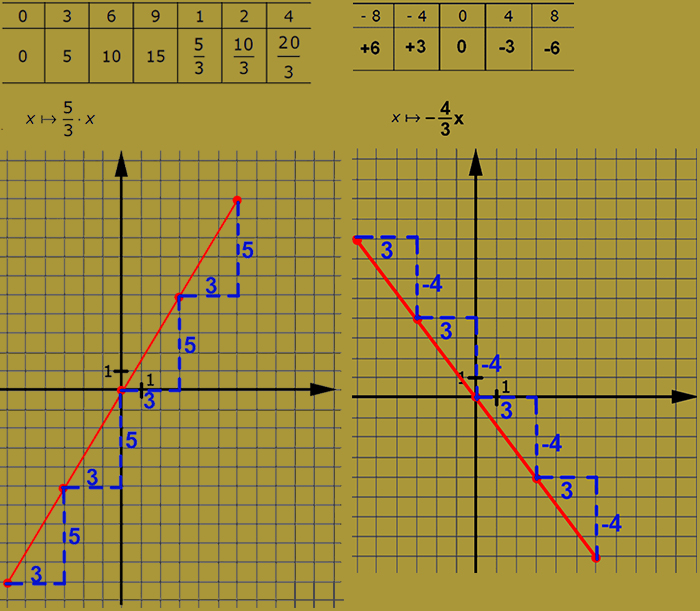
Keressük meg a kapcsolatot a grafikon és a szabály között a következő egyenes arányosságokban:
-
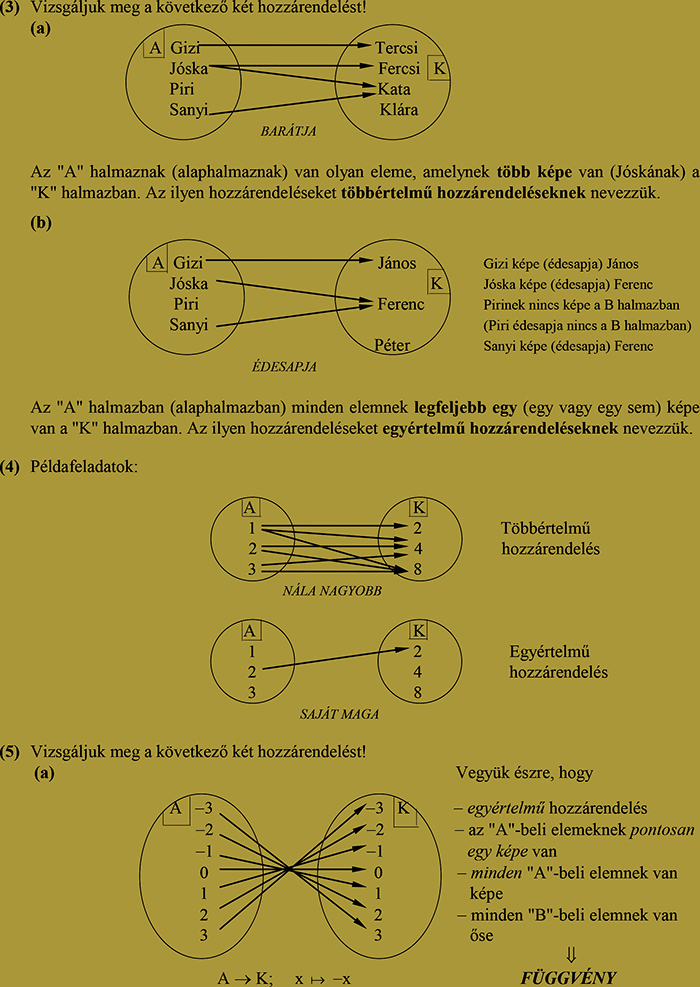
Foglaljuk össze az eddigieket:
- az egyenes arányosságok grafikonja egyenes,
- az egyenes mindig az origón halad keresztül,
- a meredekséget jelölő szám megmutatja, hogyan lehet a grafikon egyik rácsponjából a másikba eljutni;
- ha a meredekséget jelölő szám pozitív, akkor a grafikon „emelkedik”; ha negatív, akkor „lejt”.
Lássuk akkor ezek után, mindezeket figyelembe véve, hogyan ábrázolhatunk egy egyenes arányosságot értéktáblázat nélkül, pusztán hozzárendelési szabály alapján?
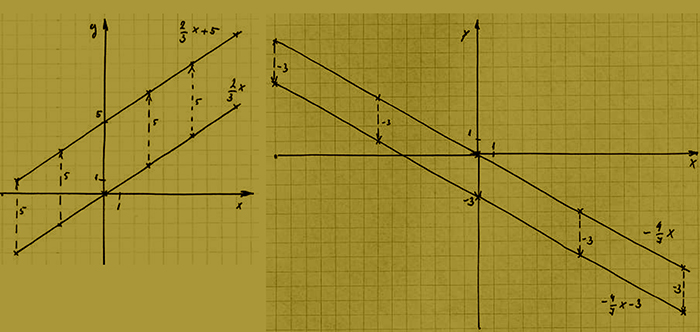
Első esetben egy növekvő függvényt kell ábrázolnunk, amelynek a meredeksége egész szám. Magunkban ezt törtté alakítjuk, mert a tört számlálója és nevezője ad információt arra vonatkozólag, hogy jussunk a grafikon egyik rácspontjából a másikba. Lépések:
- az első rácspontot tegyük az origóba, hiszen itt biztosan áthalad a grafikon,
- vízszintesen (x-tengely mentén) lépjünk annyi egységet az origótól jobbra, amennyi a meredekség nevezője,
- függőlegesen (y-tengely mentén) pedig lépjünk a számlálónak megfelelően. Figyelem! Ne felejtkezzünk el arról, ha függvény meredeksége pozitív szám (növekvő), akkor az y-tengely mentén felfelé kell lépni, ha a meredekség negatív szám (csökkenő), akkor az y-tengely mentén lefelé kell lépni.
- Így megkaptuk az egyenes két pontját, a kapott rácspontokból e lépéseket ismételve megkapjuk a grafikon tetszőleges számú pontját.
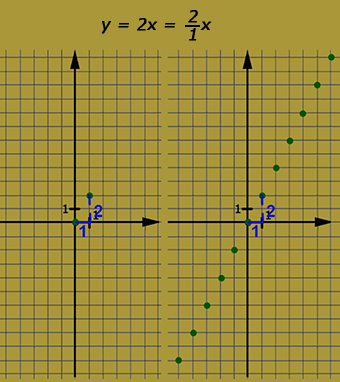
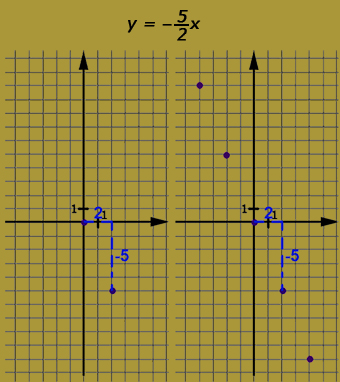
A kapott pontok egyenes arányosság esetén mindig egy egyenesre illeszkednek, de nem minden esetben köthetők össze. Ha az értelmezési tartomány (x-tengely pontjai) a racionális számok halmaza (vagy annál bővebb számhalmaz), akkor a pontok összeköthetők, mivel azok az x-tengelyen olyan végtelen sűrűn helyezkednek el, hogy a hozzájuk tartozó y-értékek egyenessé olvadnak össze. Ha az értelmezési tartomány a természetes vagy az egész számok halmaza, akkor azok az x-tengelyen elkülönülő pontok halmaza, így a hozzájuk tartozó y-értékek is elkülönülnek, nem köthetők össze, csupán egyenesre illeszthetők.
7. feladatsor

8.
Elsőfokú függvények és ábrázolásuk
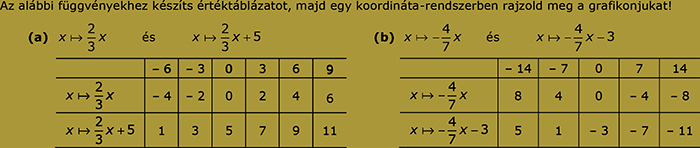


Tehát az egyenes arányosságok a az elsőfokú függvényeknek az a speciális esete, amikor b = 0.
Mindez lehetőséget ad arra is, hogy a nem egyenes arányosságot leíró függvényeket is könnyen ábrázolhatjuk:
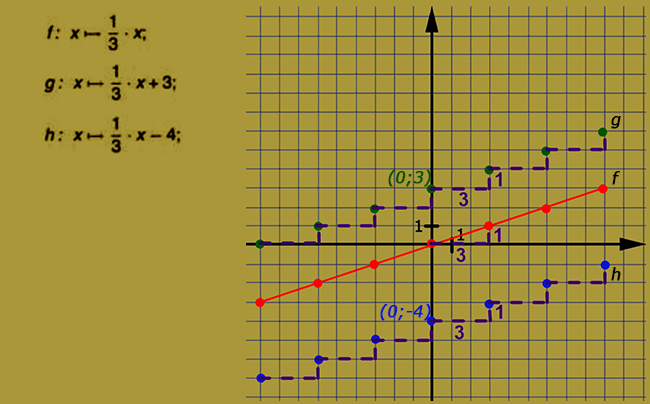
A fenti példában mindhárom függvény növekvő (m > 0), a meredekségük egyenlő. Mivel ez tulajdonképpen az x-tengellyel bezárt szögüket határozza meg, így a 3 függvény grafikonja párhuzamos.
A g(x) függvény ábrázolásánál azelső pontot, ahol a grafikon biztosan áthalad a (0, 3) pontba, a h(x) függvény esetén pedig a (0; -4) pontba kell elhelyezni, majd ezen pontokból kiindulva kell kilépegetni a grafikonok további pontjait.
9. feladatsor


10. feladatsor




11. feladatsor
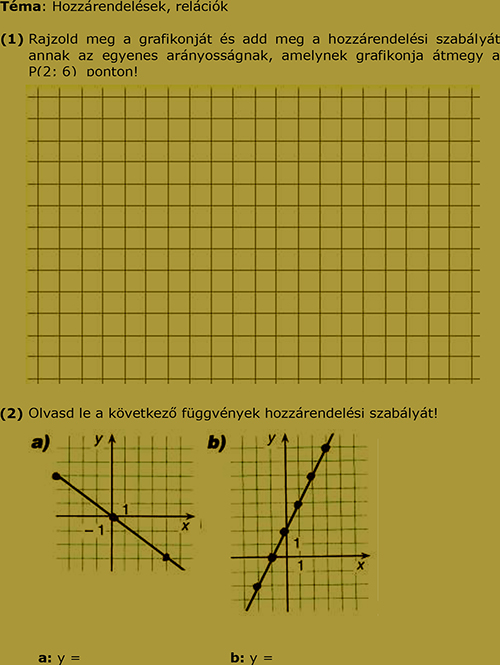

12. feladatsor

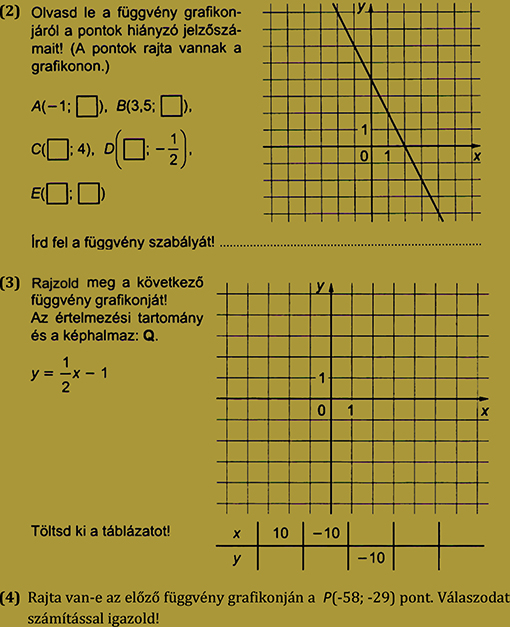
13. feladatsor
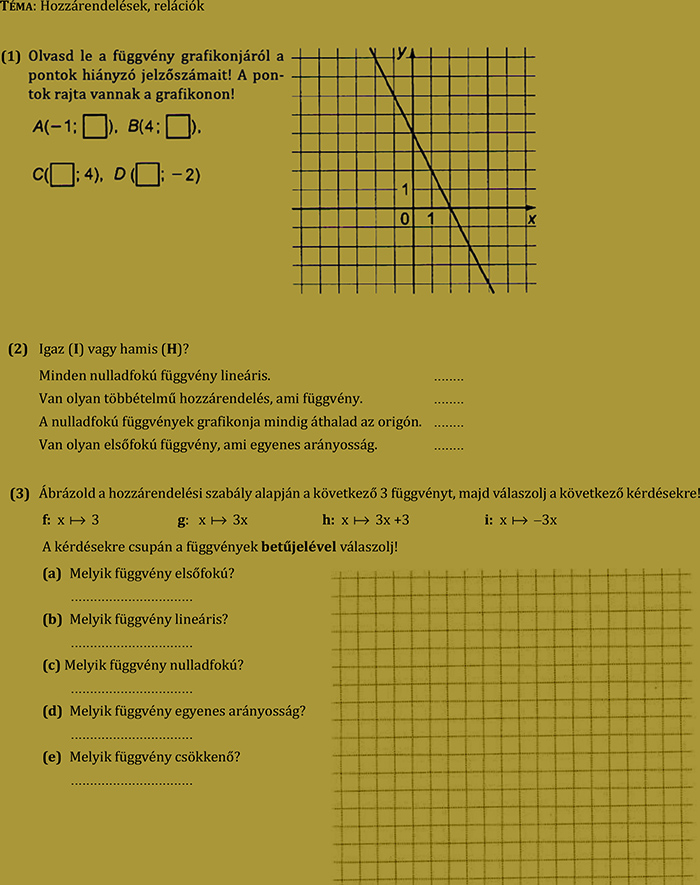
14. feladatsor


15. feladatsor
Összefoglaló kérdések

16. feladatsor
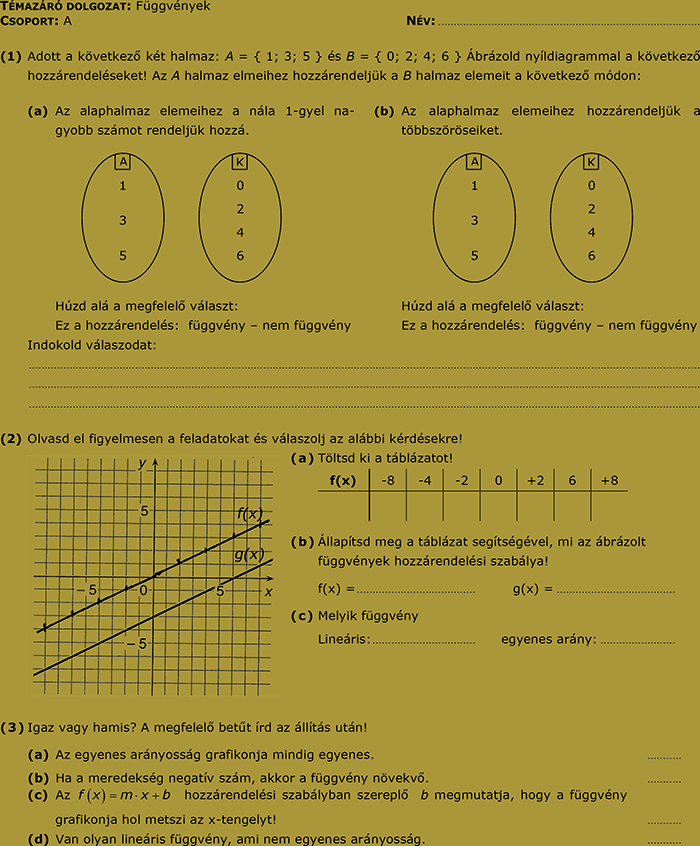
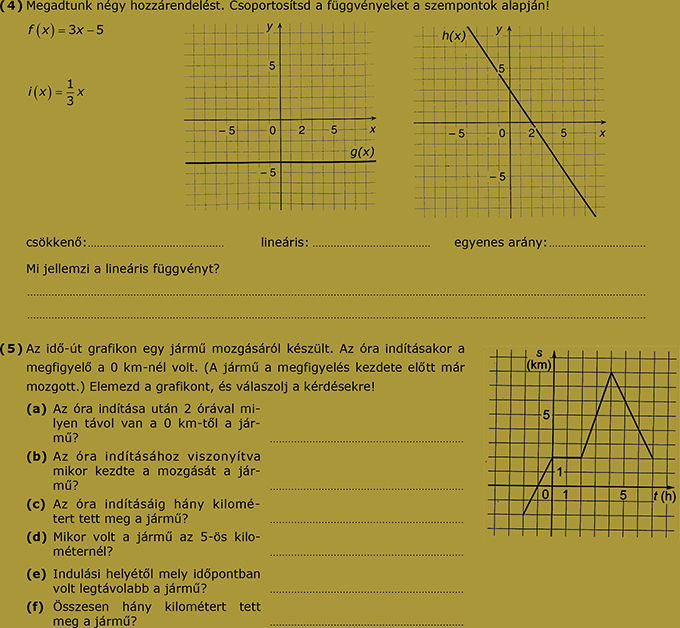
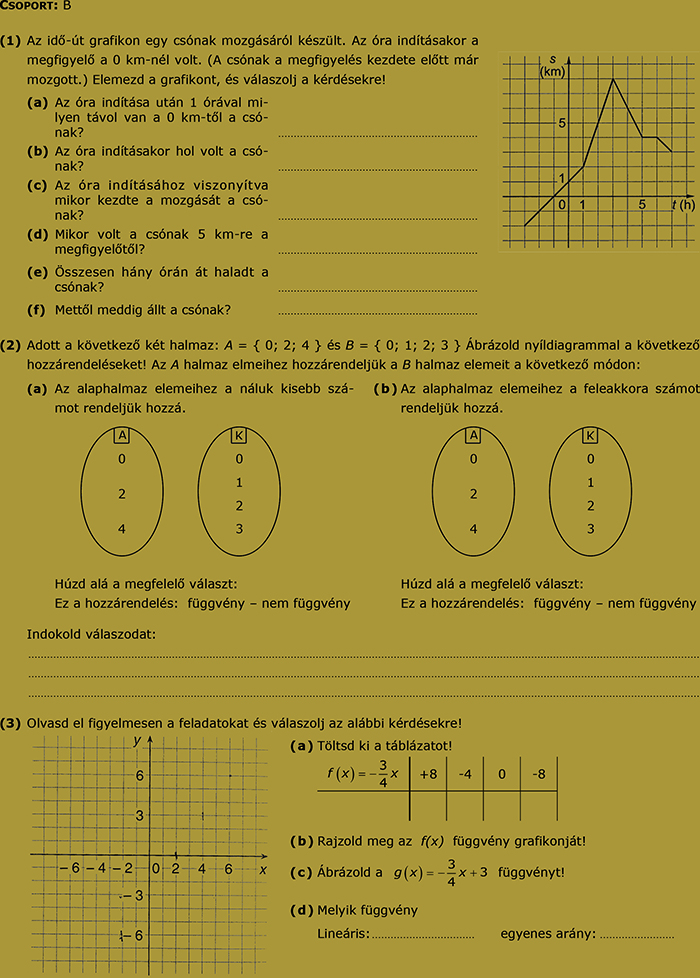

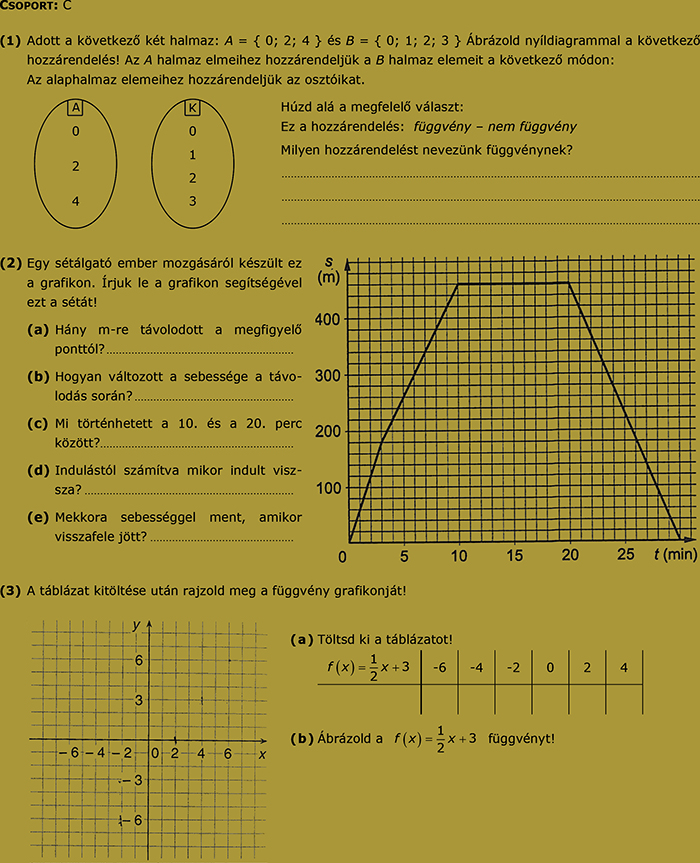
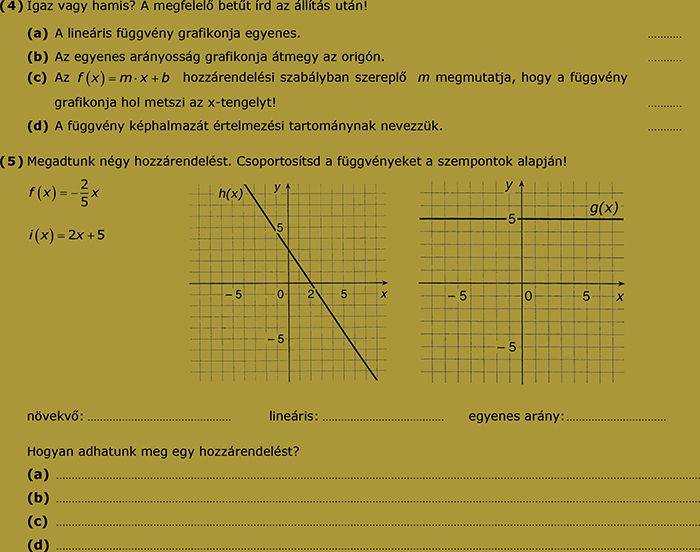
17. feladatsor